§ 11. Построение проектной линии
В практике встречаются несколько случаев построения проектной линии.
Случай первый. Проектная линия не превышает длины мерного прибора, а концы линии лежат в горизонтальной плоскости. Если измерения ведут на плоскости, то поправку за провес не вводят.
Случай второй. Проектное расстояние не превышает длины мерного прибора, но концы линии имеют значительную разность высот.
Случай третий (общий). Проектная линия значительно превышает длину мерного прибора, и концы линии имеют значительную разность высот. В этом случае разбивают линию на интервалы, меньшие длины мерного прибора. Производят измерение интервалов с расчетной (заданной) точностью. Вычисляют горизонтальные проложения интервалов и измеренной длины. Вычисляют величину домера до проектной длины. Домер откладывают рулеткой в горизонтальной плоскости со своим знаком.
Погрешности построения проектной линии. На точность построе¬ния проектной линии оказывают влияние погрешности случайного и систематического характера. Учет их не только сложен, но зачастую невозможен в условиях промплощадки шахты. Наибольшее влияние на точность измерения длины оказывают погрешности отсчитывания, которые зависят от погрешностей оцифровки мерного прибора, погрешностей фиксации измеряемого интервала, погрешностей округления и внешних условий измерений. Допустимую погрешность построения проектной линии т1 при разбивочных работах определяют по предельной погрешности АС положения точки С (см. рис. 14). Применяя принцип пропорциональности изменения погрешностей, принимают погрешность измерения всей длины
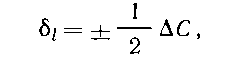
а допустимую относительную погрешность определяют из выражения
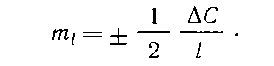
Чтобы выдержать расчетную относительную погрешность, необ¬ходимы как минимум два измерения интервала, где каждое измерение является средним арифметическим из нечетного числа измерений, т. е. из серии разностей отсчетов переднего и заднего (П — 3). Число серий обычно принимают равным пяти при измерении одним мерным прибо¬ром и трем при измерении двумя мерными приборами.
Погрешность среднего арифметического из серии измерений (П — 3) всегда должна быть меньше расчетной погрешности измеряемого интервала. Чтобы это условие соблюдалось, максимальная разница между отдельными измерениями в серии (П — 3) не должна быть больше полуторной расчетной погрешности измеряемого интервала. Например, при заданной относительной погрешности, равной 1/10 ООО, максимальная разница между отдельными измерениями в серии (П — 3) для 30-метровой длины не должна превышать 4 мм, а для 50-метровой длины (полная рулетка) эта разница не должна быть больше 7—8 мм при точности отсчетов ±1 мм.
При отсчетах по рулетке с точностью до одного миллиметра выдержать относительную погрешность менее 1/10 ООО можно только в особых условиях измерений, применяя постоянные грузы, целики и обязательно два компарированных мерных прибора. Во всех случаях, где требуется повышенная точность, следует переходить к измерениям проволоками или светодальномерами.
На практике довольно часто, сравнивая результаты двух измерений одной длины, получают относительную погрешность меньше расчетной, по которой и судят о точности измерений, не принимая во внимание методику измерений. Это заблуждение приводит к неожиданным ошибкам в последующих измерениях. Границы точности измерений длин линий следует определять только по методике измерений, которая характеризуется постоянным натяжением мерного прибора, оцифровкой, точностью отсчетов, количеством серий отсчетов, метеоусловиями и другими факторами. Например, если нивелирование выполнялось по методике 4-го класса, а величина невязок оказалась меньше, чем в нивелировании 3-го класса, это не значит, что выполнено нивели¬рование 3-го класса.
Относительная погрешность, вычисленная по результатам измерений отдельного интервала или линии из нескольких интервалов, всегда завышена, так как не учитывает многих факторов, влияющих на точность измерений. Пользоваться относительной погрешностью нужно лишь для определения границ точности элементарных измерений интервалов.